问题
解答题
已知函数f(x)=x2+1。
（1）试判断并证明该函数的奇偶性；
（2）证明函数f(x)在[0，+∞)上是单调递增的。
答案
解：（1）任给x∈R，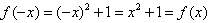
，
因此，f(x)是偶函数。
（2）任给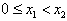
，
，
，
∴
，
∴
，
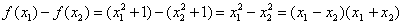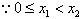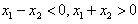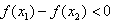所以，f(x)在[0，+∞）是增函数。
搜题请搜索小程序“爱下问搜题”
已知函数f(x)=x2+1。
（1）试判断并证明该函数的奇偶性；
（2）证明函数f(x)在[0，+∞)上是单调递增的。
解：（1）任给x∈R，，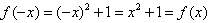
因此，f(x)是偶函数。
（2）任给，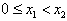
，
，
∴，
∴，
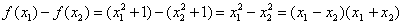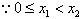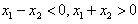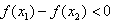所以，f(x)在[0，+∞）是增函数。