问题
选择题
已知椭圆
|
答案
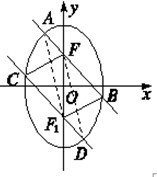
如图:两条平行直线分别经过椭圆的两个焦点,连接AF1,FD.
由椭圆的对称性可知,四边形AFDF1(其中F1是椭圆的下焦点)为平行四边形,所以AF1=FD,同理BF1=CF.
所以AF+BF+CF+DF=AF+BF+BF1+AF1=4a=8.
故选D.
已知椭圆
|

如图:两条平行直线分别经过椭圆的两个焦点,连接AF1,FD.
由椭圆的对称性可知,四边形AFDF1(其中F1是椭圆的下焦点)为平行四边形,所以AF1=FD,同理BF1=CF.
所以AF+BF+CF+DF=AF+BF+BF1+AF1=4a=8.
故选D.