问题
解答题
已知二次函数f（x）满足f（x+1）-f（x）=2x且f（0）=1。
（1）求f（x）的解析式；
（2） 当x∈[-1，1]时，不等式：f（x）>2x+m恒成立，求实数m的范围；
（3）设g（t）=f（2t+a），t∈[-1，1]，求g（t）的最大值。
答案
解：（1）令f（x）=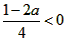
代入：
得：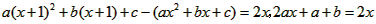
∴
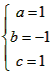∴f（x）=x2-x+1
（2）①当x∈[-1，1]时，f（x）>2x+m恒成立即：x2-3x+1>m恒成立；
令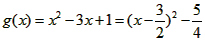
，x∈[-1，1]则对称轴：x=
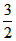∈[-1，1]，
g（x）min=g（1）=-1，∴m≤-1；
（3）g（t）=f（2t+a）=4t2+（4a-2）t+a2-a+1，t∈[-1，1]，
对称轴为：t=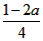
，
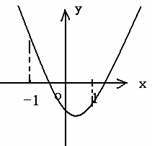
当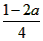
≥0时，即：a≤
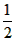；如图1，
，
；
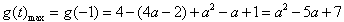②当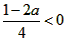时，即a>
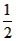；如图2，
，
g（t）max=g（1)=4+(4a-2)+a2-a+1=a2+3a+3；
综上所述：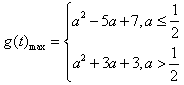
。
、电子的电势能
、电子动能
的变化关系是( )