问题
解答题
已知函数f（x）=3x2+a，g（x）=2ax+1（a∈R）
(1)证明：方程f（x）= g（x）恒有两个不相等的实数根；
(2)若函数f（x）在[0，2]上无零点，请你探究函数y= |g（x）|在[0，2]上的单调性；
(3)设F（x）= f（x）- g（x），若对任意的，恒有-1＜F（x）＜1成立，求实数a的取值范围。
答案
解：（1）“略”
（2）若函数f（x）在[0，2]上无零点，则a＞0或a＜-12
当a＞0 时，函数y= |f（x）| 在[0，2] 上的单调递增
当a＜-12 时，函数y=|f（x）| 在[0，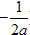
] 上的单调递减，在[
，2] 上的单调递增．
（3） 1＜a＜2