问题
解答题
已知函数f(x)=-x2+2x。
（1）判断f(x)在区间(-∞，1]上的单调性，并证明你的结论；
（2）当x∈[0，5]时，求f(x)的最大值和最小值。
答案
解：（1）f（x）在区间(-∞，1]上为增函数，
下面给予证明： 任取x1，x2∈(-∞，1]且x1＜x2，
则f(x1)-f(x2)=（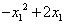
）-（
）
=
，
∵
，
∴
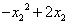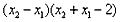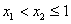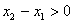，且
，
∴
，
∴
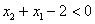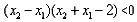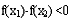，即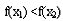
，
∴f(x)在区间(-∞，1]上是减函数。
（2）函数
的图象开口向下，对称轴为x=1，
∴f（x）在[0，1]上单调递增，在[1，5]上单调递减，
∵
，
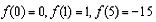∴f（x）在[0，5]上的最大值为1，最小值为-15。