问题
解答题
已知函数f（x）=-x2+8x，g（x）=6lnx+m。
(1) 求f（x）在区间[t，t+1]上的最大值h（t）；
(2)是否存在实数m使得y=f（x）的图像与y=g（x）的图像有且只有三个不同的交点？若存在，求出m的取值范围；若不存在，说明理由。
答案
解析：（1）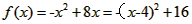
当t+1<4，即t<3时，f（x）在[t，t+1]上单调递增，
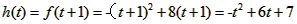
当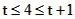
，即
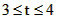时，h（t）=f（4）=16
当t>4时，f（x）在[t，t+1]上单调递减，
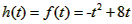
综上，h（t）=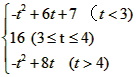
（2）函数y=f（x）的图像与y=g（x）的图像有且只有三个不同的交点，
即函数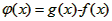
的图像与x的正半轴且只有三个不同的交点
∴
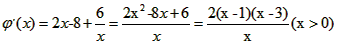
当x∈（0，1）时，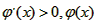
是增函数；
当x=1或x=3时，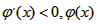
是减函数；
当x∈（3，+∞）时，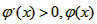
是增函数；
当x=1或x=3时，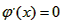
∴
∵当x充分接近0时，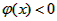
，当x充分大时，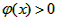
要使函数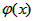
的图像与x的正半轴有三个不同的交点.必须且只需
∴
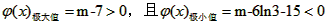
即当7<m<15-ln3，
所以，存在实数m满足题意。