问题
解答题
已知函数f(x)=x2-2x，g(x)=x2-2x，x∈[2，4]。
（1）求f(x)，g(x)函数的值域；
（2）函数H(x)=f(x-c)+g(x+c)定义域为[8，10]，求c；
（3）函数H(x)=f(x-c)+g(x+c)(c≤0)的最大值为32，求c的值。
答案
解：（1）函数f（x）的值域[-1，+∞）；函数g（x）的值域为[0，8]。
（2）设H(x)定义域M，由题意得 M={x|2≤x+c≤4}，即M={x|2-c≤x≤4-c}，
所以，有2-c=8，所以c=-6。
（3）
，
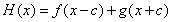
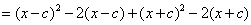
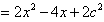因为c≤0，所以函数在[2-c，4-c]上增函数，
由已知函数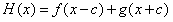
的最大值32，所以H(4-c)=24，
有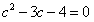
，解得c=4（舍去）或c=-1，
所以c= -1。