问题
解答题
已知抛物线y2=x+1,定点A(3,1),B为抛物线上任意一点,点P在线段AB上,且有BP:PA=1:2,当点B在抛物线上变动时,求点P的轨迹方程,并指出这个轨迹为那种曲线.
答案
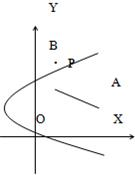
设点B的坐标(X,Y),点P的坐标为(x,y),则
x=
=X+
×31 2 1+ 1 2
,y=2X+3 3
=Y+
×11 2 1+ 1 2 2Y+1 3
∴X=
(x-1),(1)Y=3 2
(3y-1),(2)1 2
∵点B在抛物线上,∴Y2=X+1,
将(1),(2)代入此方程,得
[
(3y-1)]2=1 2
(x-1)+13 2
化简得3y2-2y-2x+1=0,
即x=
y2-y+3 2
,1 2
因此轨迹为抛物线
