若二次函数y=-x2+mx-1的图象与两端点为A(0,3)、B(3,0)的线段AB有两个不同的交点,求m的取值范围.
解:线段AB的方程为x+y=3,
由题意得方程组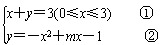 在[0,3]上有两组实数解,
在[0,3]上有两组实数解,
将①代入②,得x2-(m+1)x+4=0(0≤x≤3),
此方程有两个不同的实数根,
令f(x)=x2-(m+1)x+4,则二次函数f(x)在x∈[0,3]上有两个实根,
故有: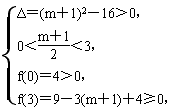
解得:3<m≤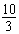 ,
,
故m的取值范围是(3,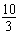 ].
].
若二次函数y=-x2+mx-1的图象与两端点为A(0,3)、B(3,0)的线段AB有两个不同的交点,求m的取值范围.
解:线段AB的方程为x+y=3,
由题意得方程组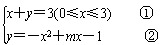 在[0,3]上有两组实数解,
在[0,3]上有两组实数解,
将①代入②,得x2-(m+1)x+4=0(0≤x≤3),
此方程有两个不同的实数根,
令f(x)=x2-(m+1)x+4,则二次函数f(x)在x∈[0,3]上有两个实根,
故有: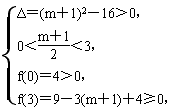
解得:3<m≤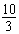 ,
,
故m的取值范围是(3,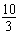 ].
].