问题
解答题
二次函数f(x)的最小值为1,且f(0)=f(2)=3。
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围.
答案
解:(1)∵f(x)为二次函数且f(0)=f(2),
∴对称轴为x=1,
又∵f(x)最小值为1,
∴可设f(x)=a(x-1)2+1,(a>0)
∵f(0)=3,
∴a=2,
∴f(x)=2(x-1)2+1,即f(x)=2x2-4x+3。
(2)由条件知2a<1<a+1,∴0<a<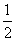 。
。
