问题
解答题
已知抛物线y 2=2px及定点A(a,b),B(-a,0),(ab≠0,b 2≠2pa).M是抛物线上的点,设直线AM,BM与抛物线的另一交点分别为M1,M2.
求证:当M点在抛物线上变动时(只要M1,M2存在且M1≠M2),直线M1M2恒过一个定点.并求出这个定点的坐标.
答案
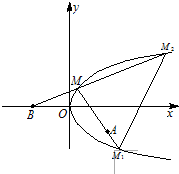
证明:设M(
,m).M1(m2 2p
,m1),M2(m12 2p
,m2),m22 2p
则A、M、M1共线,得
=b-m m1-m
,即b-m=a- m2 2p
-m12 2p m2 2p 2pa-m2 m1+m
.2pa-m2 m1+m
∴m1=
,同法得m2=2pa-bm b-m
;2pa m
∴M1M2所在直线方程为
=y-m2 m1-m2
,即(m1+m2)y=2px+m1m2.2pa-m22 m12-m22
消去m1,m2,得2paby-bm2y=2pbmx-2pm2x+4p2a2-2pabm.(1)
分别令m=0,1代入,得x=a,y=
,2pa b
以x=a,y=
代入方程(1)知此式恒成立.2pa b
即M1M2过定点(a,
)2pa b
