问题
解答题
已知二次函数f(x)的最小值为1，且f(0)= f(2)=3。
（1）求f(x)的解析式；
（2）若f(x)在区间[2a，a+1]上不单调，求实数a的取值范围；
（3）在区间[-1，1]上，y=f(x)的图象恒在y=2x+2m+1的图象上方，试确定实数m的取值范围。
答案
解：（1）由已知，设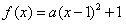
（a＞0），
由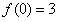
，得a=2，
故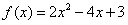
。
（2）要使函数不单调，则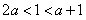
，即
。
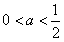（3）由已知，即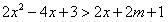
，
化简，得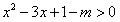
，
设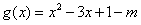
，则只要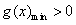
，
而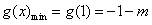
，
解得：m＜-1，
即实数m的取值范围是（-∞，-1）。