问题
解答题
已知二次函数y=f(x)的定义域为R,f(1)=2,在x=t处取得最值,若y=g(x)为一次函数,
且f(x)+g(x)=x2+2x-3
(1) 求y=f(x)的解析式;
(2) 若x∈[-1,2]时,f(x)≥-1恒成立,求t的取值范围;
答案
解:(1) 设f(x)=a(x-t)2+b, 又因为f(x)+g(x)=x2+2x-3 所以a=1,即f(x)=(x-t)2+b ,
又f(1)=2 代入得(1-t)2+b=2,得b= -t2+2t+1
所以f(x)=x2-2tx+2t+1;
(2)利用二次函数图象求函数f(x)在区间内的最小值,只需f(x)min≥-1即可。
①当t≤-1时,f(x)min≥-1不成立,
②当-1<t<2时,f(x)min= -t2+2t+1-1得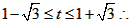
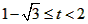
③当t≥2时,f(x)min=f(2)≥-1,得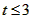 ,∴
,∴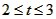
综上t的取值范围是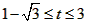 。
。
