问题
解答题
已知函数f(x)=x2+(2a-1)x-3，
(Ⅰ)当a=2，x∈[-2，3]时，求函数f(x)的值域；
(Ⅱ)若函数f(x)在[-1，3]上的最大值为1，求实数a的值．
答案
解：(Ⅰ)当a=2时，f(x)=x2+3x-3，x∈[-2，3]，
对称轴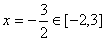
，
∴
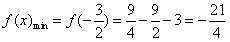，f(x)max=f(3)=15，
∴值域为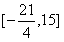
。
(Ⅱ)对称轴为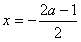
，
i)当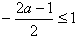
，即
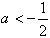时，f(x)max=f(3)=6a+3，
∴6a+3=1，即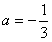
满足题意；
ii)当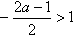
，即
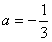时，f(x)max=f(-1)=-2a-1，
∴-2a-1=1，即a=-1满足题意；
综上可知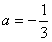或-1．