问题
解答题
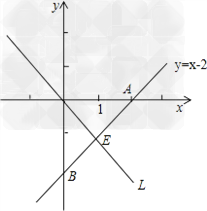
直线y=x﹣2分别交x轴、y轴于A、B两点,原点为O
(1)求△AOB的面积;
(2)求O到直线y=x﹣2的距离;
(3)是否存在过△AOB的顶点的直线L,把△AOB分成面积相等的两部分,若存在,写出直线L的解析式.
答案
解:(1)∵直线y=x﹣2分别交x轴、y轴于A、B两点,
∴A、B点的坐标分别为(2,0)、(0,﹣2),S△AOB=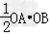 =
=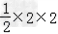 =2;
=2;
(2)从图中不难发现O到直线y=x﹣2的距离即为△AOB边AB边上的高,
∴AB= =
= ,
,
∴△AOB边AB边上的高OE=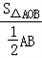 =
=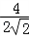 =
= ;
;
(3)①当过△AOB顶点O时,如图所示,E为直线L与直线AB的交点,由题意及图知E为线段AB的中点,
∴E点的坐标为(1,﹣1),则直线L的解析式为y=﹣x,
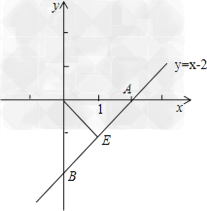
②当过△AOB顶点A时,如图所示,E为直线L与y轴的交点,
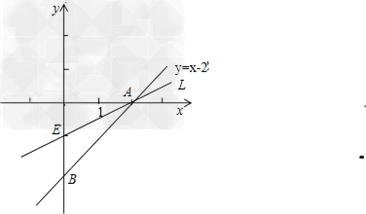
由题意及图知E为线段OB的中点,
∴E点的坐标为(0,﹣1),
则直线L的解析式为y﹣(﹣1)= x,即
x,即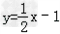 ,
,
③当过△AOB顶点B时,
如图所示,E为直线L与x轴的交点,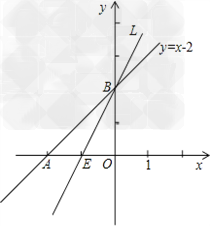
由题意及图知E为线段OA的中点,
∴E点的坐标为(﹣1,0),则直线L的解析式为y+2=2x,
即y=2x﹣2.