问题
选择题
已知抛物线C的方程为x2=
|
答案
解:如图,设过A的直线方程为y=kx-1,与抛物线方程联立得x2- kx+
kx+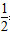 =0,
=0,
△=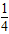 k2-2=0,k=
k2-2=0,k=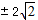 ,求得过A的抛物线的切线与y=3的交点为(±
,求得过A的抛物线的切线与y=3的交点为(±  ,3),
,3),
则当过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,实数t的取值范围是(-∞,- 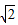 )∪(
)∪( 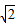 ,+∞),
,+∞),
故选D.
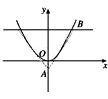
已知抛物线C的方程为x2=
|
解:如图,设过A的直线方程为y=kx-1,与抛物线方程联立得x2- kx+
kx+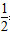 =0,
=0,
△=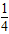 k2-2=0,k=
k2-2=0,k=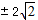 ,求得过A的抛物线的切线与y=3的交点为(±
,求得过A的抛物线的切线与y=3的交点为(±  ,3),
,3),
则当过点A(0,-1)和点B(t,3)的直线与抛物线C没有公共点,实数t的取值范围是(-∞,- 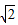 )∪(
)∪( 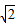 ,+∞),
,+∞),
故选D.
