问题
解答题
已知函数f(x)=x3-bx2+2cx的导函数的图象关于直线x=2对称，
(Ⅰ)求b的值；
(Ⅱ)若函数f(x)无极值，求c的取值范围；
(Ⅲ)若f(x)在x=t处取得极小值，记此极小值为g(t)，求g(t)的定义域和值域。
答案
解：(Ⅰ)f′(x)=3x2-2bx+2c，
∵函数f′(x)的图象关于直线x=2对称，
∴
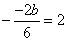，即b=6．
(Ⅱ)由(Ⅰ)知，f(x)=x3-6x2+2cx，
f′(x)=3x2-12x+2c=3(x-2)2+2c-12，
当c≥6时，f′(x)≥0，此时f(x)无极值。
(Ⅲ)当c＜6时，f′(x)=0有两个互异实根x1，x2，
不妨设x1＜x2，则x1＜2＜x2，
当x＜x1时，f′(x)＞0，f(x)在区间(-∞，x1)内为增函数；
当x1＜x＜x2时，f′(x)＜0，f(x)在区间(x1，x2)内为减函数；
当x＞x2时，f′(x)＞0，f(x)在区间(x2，+∞)内为增函数，
所以f(x)在x=x1处取极大值，在x=x2处取极小值，
因此，当且仅当c＜6时，函数f(x)在x=x2处存在唯一极小值，所以t=x2＞2，
于是g(t)的定义域为(2，+∞)，
由f′(t)=3t2-12t+2c=0，得2c=-3t2+12t，
于是g(t)=f(t)=t3-6t2+(-3t2+12t)t=-2t3+6t2，t∈(2，+∞)，
当t＞2时，g′(t)=-6t2+12t=-6t(t-2)＜0，
所以函数g(t)在区间(2，+∞)内是减函数，故g(t)的值域为(-∞，8)。