设椭圆
(I)若∠AF1F2=α,∠AF2F1=β,试用α,β表示椭圆的离心率e; (II)设
|
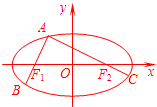
(I)设F1(-c,0),F2(c,0).在△AF1F2中,由正弦定理得
=|AF1| sinβ
=|AF1| sinα
,|F1F2| sin(α+β)
即|AF1|=
,|AF2|=sinβ|F1F2| sin(α+β)
,sinα|F1F2| sin(α+β)
所以2a=|AF1|+|AF2|=
+sinβ|F1F2| sin(α+β)
,sinα|F1F2| sin(α+β)
=2c(
+sinβ sin(α+β)
)=2c•sinα sin(α+β)
,sinα+sinβ sin(α+β)
得e=
.sin(α+β) sinα+sinβ
(II)设A(x0,y0),B(x1,y1),C(x2,y2).
①当y0=0时,λ1+λ2=2
=a2 +c2 a2-c2
;当AB或AC与x轴垂直时,λ1+λ2=2(1+e2) 1-e2
.2(1+e2) 1-e2
②当AB,AC都不与x轴垂直且y0≠0时,AC的方程为y=
(x-c),y0 x0-c
由
,y=
(x-c)y0 x0-c
+x2 a2
=1y2 b2
消x得[b2(x0-c)2+a2y02]y2+2b2y0(x0-c)y+c2b2y02-a2b2y02=0.
由韦达定理得 y2y0=
,c2b2y02-a2b2y02 b2(x0-c)2+a2y02
所以y2=
,c2b2y0-a2 b2y0 b2(x0-c)2+a2y02
所以 λ2=
=-|AF2| |F2C|
=-y0 y2
,b2(x0-c)2+a2y02 c2b2-a2b2
同理可得λ1=
=-|AF1| |F1C|
=-(y0 y1
+b2(x0-c)2+a2y02 c2b2-a2b2
],b2(x0+c)2+a2y02 c2b2-a2b2
故λ1+λ2=
.2(1+e2) 1-e2
