问题
解答题
已知函数f(x)=x2-4x-4。
（1）若函数定义域为[3，4]，求函数值域；
（2）若函数定义域为[-3，4]，求函数值域；
（3）当x∈[a-1，a]时，y的取值范围是[1，8]，求a。
答案
解：（1）f(x)=(x-2)2-8开口向上，对称轴x=2，
∴当x∈[3，4]时，f(x)为增函数，最小值f(3)=-7，最大值f(4)=-4，
∴值域为[-7，-4]．
（2）f(x)=(x-2)2-8在[-3，2]上是减函数，在[2，4]上是增函数，
∴最小值为f(2)=-8，
又f(-3)=17，f(4)=-4，
(也可以通过比较-3和4哪一个与对称轴x=2的距离远则哪一个对应函数值较大，开口向下时同样可得出)
∴最大值为17，值域为[-8，17]．
（3）∵f(x)=(x-2)2-8，当x∈[a-1，a]时，y的取值范围是[1，8]，
∴2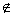
[a-1，a]，
当a＜2时，函数f(x)在[a-1，a]上是减函数，
∴
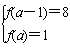，∴a=-1；
当a-1＞2，即a＞3时，f(x)在[a-1，a]上是增函数，
则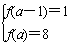
，∴a=6；
综上，得a=-1或a=6。