问题
解答题
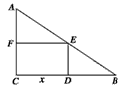
一块形状为直角三角形的铁皮,直角边长分别为40cm与60cm现将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪法,才能使剩下的残料最少?
答案
如图,剪出的矩形为CDEF,设CD=x,CF=y,则AF=40-y,
∵△AFE∽△ACB,
∴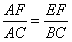 ,即
,即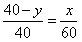 ,
,
∴y=40-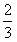 x,
x,
剩下的残料面积为
S=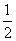 ×60×40-x·y=
×60×40-x·y=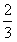 x2-40x+1200=
x2-40x+1200=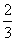 (x-30)2+600,
(x-30)2+600,
∵0<x<60,
∴当x=30时,S取最小值为600,这时y=20,
∴在边长60cm的直角边CB上截CD=30cm,
在边长为40cm的直角边AC上截CF=20cm时,能使所剩残料最少.