问题
解答题
商场销售某一品牌的羊毛衫,购买人数n是羊毛衫标价x的一次函数,标价越高,购买人数越少。已知标价为每件300元时,购买人数为零;标价为每件225元时,购买人数为75人;若这种羊毛衫的成本价是100元/件,商场以高于成本价的相同价格(标价)出售,
问:(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
答案
解:(1)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,则n=kx+b(k<0),
∴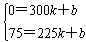 ,∴
,∴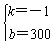 ,
,
∴n=-x+300,
y=-(x-300)·(x-100)=-(x-200)2+10000,x∈(100,300],
∴x=200时,ymax=10000,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(2)由题意得,-(x-300)·(x-100)=10000×75%,
∴x2-400x+30000=-7500,
∴x2-400x+37500=0,
∴(x-250)(x-150)=0,
∴x1=250,x2=150,
所以当商场以每件150元或250元出售时,可获得最大利润的75%。
