问题
解答题
已知定直线l及定点A(A不在l上),n为过点A且垂直于l的直线,设N为l上任意一点,线段AN的垂直平分线交n于B,点B关于AN的对称点为P,求证:点P的轨迹为抛物线.
答案
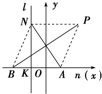
证明:如图所示,建立平面直角坐标系,并且连结PA,PN,NB.
由题意知PB垂直平分AN,且点B关于AN的对称点为P,
∴AN也垂直平分PB.
∴四边形PABN为菱形,
∴PA=PN.
∵AB⊥l,∴PN⊥l.
故点P符合抛物线上点的条件:到定点A的距离和到定直线l的距离相等,
∴点P的轨迹为抛物线.
