已知椭圆
(1)若弦AB恰好被点P平分,求直线AB的方程; (2)当原点O到直线AB的距离取最大值时,求△AOB的面积. |
(1).设A(x1,y1),B(x2,y2),直线AB的斜率为k,
由A、B在椭圆上,得
+x 21 9
=1 ①y 21 4
+x 22 9
=1 ②y 22 4
又∵P(2,1)是AB的中点,∴
.x1+x2=4 y1+y2=2
由①-②得
+(x1+x2)(x1-x2) 9
=0,(y1+y2)(y1-y2) 4
∴k=
=-y1-y2 x1-x2
.8 9
∴直线AB的方程为y-1=-
(x-2),即 8x+9y-25=0;8 9
(2).当原点O到直线AB的距离取最大值时 满足:OP⊥AB.
∵kOP=
,∴kAB=-2,1 2
∴直线AB的方程为 y-1=-2(x-2),即 2x+y-5=0.
联立方程组
得 40x2-180x+189=0,2x+y-5=0
+x2 9
=1y2 4
设A(x1,y1),B(x2,y2),则
,x1+x2= 9 2 x1x2= 189 40
∴|AB|=1+k2
=(x1+x2)2-4x1x2 3 2
.3
∴S△AOB=
|OP||AB|=1 2 3 4
.15

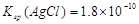 ,则在0.1mol·L-1AlCl3溶液中,Ag+的物质的量浓度最大可达到
,则在0.1mol·L-1AlCl3溶液中,Ag+的物质的量浓度最大可达到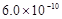 mol·L-1
mol·L-1