问题
解答题
定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M＞0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界，已知函数f(x)=1+x+ax2，
(Ⅰ)当a=-1时，求函数f(x)在(-∞，0)上的值域，并判断函数f(x)在(-∞，0)上是否为有界函数，并说明理由；
(Ⅱ)若函数f(x)在x∈[1，4]上是以3为上界的有界函数，求实数a的取值范围。
答案
解：(Ⅰ)当a=-1时，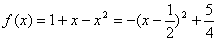
，
∴f(x)在x∈(-∞，0)上单调递增，
∴
，
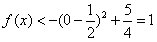故函数f(x)在(-∞，0)上的值域为(-∞，1)，
又∵f(x)＜1，
∴|f(x)|∈[0，+∞)，
∴不存在常数M＞0，使|f(x)|≤M都成立，
故函数f(x)在(-∞，0)上不是有界函数．
(Ⅱ)若函数f(x)在[1，4]上是以3为上界的有界函数，
则|f(x)|≤3在[1，4]上恒成立，即-3≤f(x)≤3，
∴-3≤ax2+x+1≤3，
∴
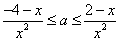，即
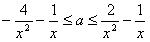在x∈[1，4]上恒成立，
∴
，
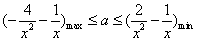令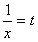
，则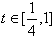
，
∴
，
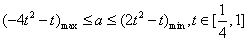令g(t)=-4t2-t，则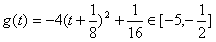
，
令h(t)=2t2-t，
则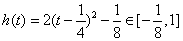
，
∴实数a的取值范围为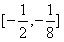
。