问题
解答题
若cos2θ+2msinθ-2m-2<0恒成立,试求实数m的取值范围。
答案
解:令sinθ=t,则-1≤t≤1,
要使cos2θ+2msinθ-2m-2<0恒成立,
即sin2θ-2msinθ+2m+1>0恒成立,
设f(t)=t2-2mt+2m+1,则只要f(t)>0在[-1,1]上恒成立即可,
由于f(t)=(t-m)2+2m+1-m2(-1≤t≤1),
所以只要f(t)的最小值大于零即可,
若m<-1,则当t=-1时,f(t)min=2+4m,
令2+4m>0,得m>-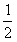 ,这与m<-1矛盾,故舍去;
,这与m<-1矛盾,故舍去;
若-1≤m≤1,则当t=m时,f(t)min=-m2+2m+1,
令-m2+2m+1>0,解得1-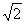 <m<1+
<m<1+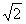 ,
,
∴1-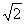 <m≤1;
<m≤1;
若m>1,则当t=1时,f(t)min=2>0,∴m>1;
综上所述,m>1-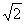 。
。
