问题
解答题
设a为实数，函数f(x)=x2+|x-a|+1，x∈R，
(1)讨论f(x)的奇偶性；
(2)求f(x)的最小值．
答案
解：(1)当a=0时，f(-x)=(-x)2+|-x|+1=f(x)，此时f(x)为偶函数；
当a≠0时，f(a)=a2+1，f(-a)=a2+2|a|+1，
∴f(-a)≠f(a)，f(-a)≠-f(a)，
此时函数f(x)既不是奇函数也不是偶函数．
(2)①当x≤a时，函数f(x)=x2-x+a+1=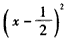
+a
，
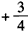若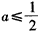
，则函数f(x)在(-∞，a]上单调递减，
∴函数f(x)在(-∞，a]上单调递减，
∴函数f(x)在(-∞，a]上的最小值为f(a)=a2+1；
若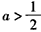
，函数f(x)在(-∞，a]上的最小值为
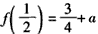，且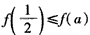
；
②当x≥a时，函数f(x)=x2+x-a+1=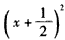
-a+
，
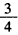若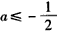
，则函数f(x)在[a，+∞)上最小值为
，且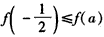
；
若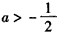
，则函数f(x)在[a，+∞)上单调递减，
∴函数f(x)在[a，+∞)上的最小值是f(a)=a2+1；
综上，当a≤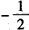
时，函数f(x)的最小值是
；
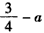当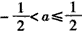
时，函数f(x)的最小值是a2+1；
当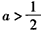
时，函数f(x)的最小值是
。