问题
解答题
画出函数y=-x2+2|x|+3的图象，并指出函数的单调区间。
答案
解：y=-x2+2|x|+3=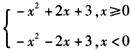
，
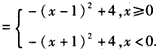函数图象如下图，
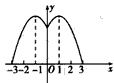
由图象可知，在(-∞，-1)和[0，1]上，函数是增函数，
在[-1，0]和(1，+∞)上，函数是减函数．
搜题请搜索小程序“爱下问搜题”
画出函数y=-x2+2|x|+3的图象，并指出函数的单调区间。
解：y=-x2+2|x|+3=，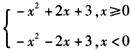
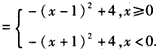函数图象如下图，
由图象可知，在(-∞，-1)和[0，1]上，函数是增函数，
在[-1，0]和(1，+∞)上，函数是减函数．