问题
解答题
已知函数f（x）=ax2+a2x+2b-a3，当x∈（-2，6）时，f（x）>0；当x∈（-∞，-2）∪（6，+∞）时，f（x）<0，求f（x）的解析式。
答案
解：据题意，x1=-2，x2=6是方程ax2+a2x+2b-a3=0的两根
由韦达定理知
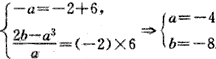
故f（x）=-4x2+16x+48。
搜题请搜索小程序“爱下问搜题”
已知函数f（x）=ax2+a2x+2b-a3，当x∈（-2，6）时，f（x）>0；当x∈（-∞，-2）∪（6，+∞）时，f（x）<0，求f（x）的解析式。
解：据题意，x1=-2，x2=6是方程ax2+a2x+2b-a3=0的两根
由韦达定理知
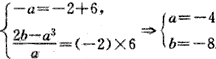
故f（x）=-4x2+16x+48。