问题
解答题
已知函数f(x)=x2+4ax+2a+6，
(1)若函数f(x)的值域为[0，+∞)，求a的值；
(2)若函数f(x)的函数值均为非负数，求g(a)=2-a|a+3|的值域．
答案
解：(1)∵函数的值域为[0，+∞)，
∴Δ=16a2-4(2a+6)=0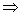
2a2-a-3=0
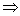a=-1或a=
。
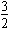(2)∵对一切x∈R函数值均为非负，
∴Δ=8(2a2-a-3)≤0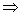
-1≤a≤
，
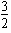∴a+3＞0，
∴g(a)=2-a|a+3|=-a2-3a+2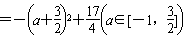
，
∵二次函数g(a)在[-1，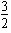
]上单调递减，
∴
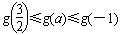，即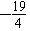
≤g(a)≤4，
∴g(a)的值域为[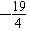
，4]．