问题
解答题
已知a,b,c,d是不全为零的实数,函数f(x)=bx2+cx+d,g(x)=ax3+bx2+cx+d。方程f(x)=0有实数根,且f(x)=0的实数根都是g(f(x))=0的根;反之,g(f(x))=0的实数根都是f(x)=0的根。
(1)求d的值;
(2)若a=0,求c的取值范围;
(3)若a=1,f(1)=0,求c的取值范围。
答案
解:(1)设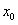 是 是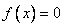 的根,那么 的根,那么 , , |
则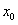 是 是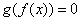 的根, 的根, |
则 即 即 , , |
所以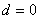 。 。 |
(2)因为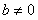 |
所以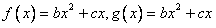 |
则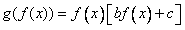 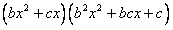 =0的根也是 =0的根也是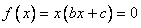 的根 的根 |
(a)若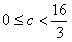 ,则 ,则 |
此时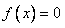 的根为0,而 的根为0,而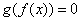 的根也是0, 的根也是0, |
所以 ; ; |
(b)若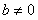 ,则 ,则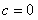 时, 时,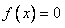 的根为0,而 的根为0,而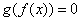 的根也是0, 的根也是0, |
当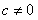 时,
时,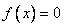 的根为0和
的根为0和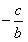 ,
,
而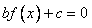 的根不可能为0和
的根不可能为0和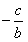 ,
,
所以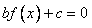 必无实数根,
必无实数根,
所以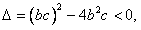
所以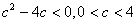 ,
,
从而
所以当![]() 时,
时,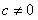 ;
;
当 时,
时,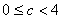 。
。
(3)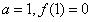 ,所以
,所以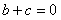
即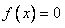 的根为0和1,
的根为0和1,
所以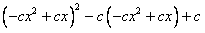 =0必无实数根,
=0必无实数根,
(a)当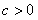 时,
时,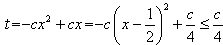
即函数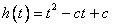 在
在 ,
,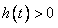 恒成立
恒成立
又
所以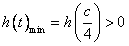
即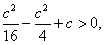
所以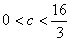 ;
;
(b)当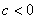 时,
时,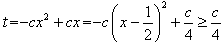
即函数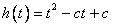 在
在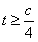 ,
, 恒成立
恒成立
又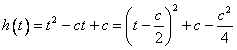
所以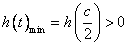 ,
,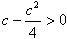 ,而
,而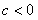
所以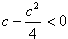
所以c不可能小于0。
(c)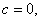 则
则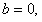 这时
这时 的根为一切实数,而
的根为一切实数,而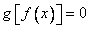 ,
,
所以 符合要求。
符合要求。
所以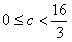 。
。
