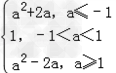问题
解答题
已知函数f(x)=x2﹣2ax+a2﹣1.
(1)若f(1)=3,求实数a的值;
(2)若函数f(x)在区间[0,2]上是单调的,求实数a的取值范围;
(3)当x∈[﹣1,1]时,求函数f(x)的最小值g(a).
答案
解:(1)∵f(x)=x2﹣2ax+a2﹣1.
又∵f(1)=3,
即1﹣2a+a2﹣1=3
即a2﹣2a﹣3=0
解得a=﹣1,或a=3
(2)∵函数f(x)=x2﹣2ax+a2﹣1的图象是开口向上,
且以x=a为对称轴的抛物线
又∵函数f(x)在区间[0,2]上是单调的,
则区间[0,2]在对称轴的同一侧
故a≤0或a≥2
(3)当a≤﹣1时,函数在[﹣1,1]为增函数,
此时函数f(x)的最小值
g(a)=f(﹣1)=a2+2a
当﹣1<a<1时,函数在[﹣1,a]上递减,在[a,1]为增函数,
此时函数f(x)的最小值g(a)=f(a)=﹣1
当a≥1时,函数在[﹣1,1]为减函数,
此时函数f(x)的最小值g(a)=f(1)=a2﹣2a
故g(a)=