问题
填空题
在△ABC中, AB=AC=2,BD⊥AC,D为垂足,若∠ABD=30°,则BC长为____ _.
答案
2或2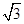 .
.
题目分析:分为两种情况,画出图形,求出AD、CD的长,根据勾股定理求出BD,再根据勾股定理求出BC即可.
试题解析:分为两种情况:① 如图1,
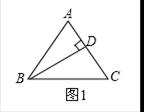
∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=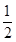 AB=1,
AB=1,
∴CD=2-1=1,
由勾股定理得:BD=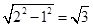 ,
,
由勾股定理得:BC=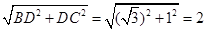 ;
;
②如图2,
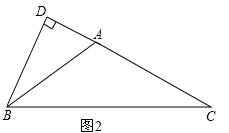
∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=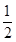 AB=1,∴CD=2+1=3,
AB=1,∴CD=2+1=3,
由勾股定理得:BD=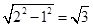 ,
,
由勾股定理得:BC= ;
;
考点: 1.含30度角的直角三角形;2.等腰三角形的性质;3.勾股定理.

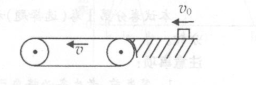
 =0.20,当传送带长度为L="12" m时,行李包从滑上水平传送带的右端到左端的时间刚好为t="2" s皮带轮与皮带之间始终不打滑.不计空气阻力,g取10 m/s2.求行李包的初速度vo.
=0.20,当传送带长度为L="12" m时,行李包从滑上水平传送带的右端到左端的时间刚好为t="2" s皮带轮与皮带之间始终不打滑.不计空气阻力,g取10 m/s2.求行李包的初速度vo.