问题
解答题
已知二次函数f（x）=x2-（m+2）x+m+2（x∈R）同时满足：①不等式f（x）≤0的解集有且只有一个元素；②在定义域内存在x1，x2，使得x1+x2=0，但f（x1）≠f（x2）。设数列{an}的前n项和Sn=f（n）。
（1）求f（x）的表达式；
（2）求数列{an}的通项公式。
答案
解：（1）∵f（x）≤0的解集有且只有一个元素，
∴Δ=[-（m+2）]2-4（m+2）=0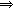
m=-2或m=2
当m=-2时，函数f（x）=x2是一个偶函数，故不存在x1，x2，使得x1+x2=0，且f（x1）≠f（x2）
当m=2时，函数f（x）=x2-4x+4，在定义域内存在x1，x2，使得x1+x2=0，且f（x1）≠f（x2），
故f（x）=x2-4x+4。
（2）由（1）可知Sn=n2-4n+4，
当n=1时，a1=S1=1，
当n≥2时，an=Sn-Sn-1=（n2-4n+4）-[（n-1）2-4（n-1）+4]=2n-5
∴
。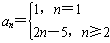