问题
解答题
已知函数f(x)=x3+3ax-1，g(x)=f′(x)-ax-5，其中f′(x)是的f(x)的导函数，
（Ⅰ）对满足-1≤a≤1的一切a的值，都有g(x)＜0，求实数x的取值范围；
（Ⅱ）设a=-m2，当实数m在什么范围内变化时，函数y=f(x)的图像与直线y=3只有一个公共点。
答案
解：（Ⅰ）由题意，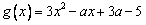
，
令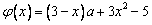
，-1≤a≤1，
对-1≤a≤1，恒有g(x)＜0，即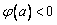
，
∴
，解得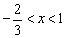
；
故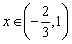
时，对满足-1≤a≤1的一切a的值，都有g(x)＜0；
（Ⅱ）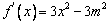
，
①当m=0时，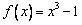
的图象与直线y=3只有一个公共点；
②当m≠0时，列表：
∴
，
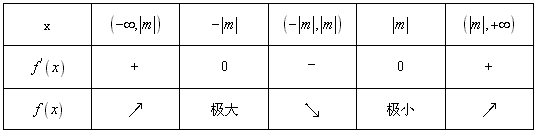
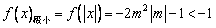又∵f(x)的值域是R，且在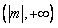
上单调递增，
∴当x＞|m|时函数y=f(x)的图象与直线y=3只有一个公共点；
当x＜|m|时，恒有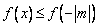
，
由题意得
，即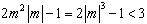
，
解得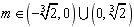
；
综上，m的取值范围是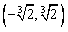
。