问题
解答题
求函数y=7-4sinxcosx+4cos2x-4cos4x的最大值与最小值．
答案
解：
，
由于函数
在[-1，1]上的最大值为zmax=
，
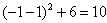最小值为
，
故当sin2x=-1时，y取得最大值10；当sin2x=1时，y取得最小值6。
搜题请搜索小程序“爱下问搜题”
求函数y=7-4sinxcosx+4cos2x-4cos4x的最大值与最小值．
解：
，
由于函数在[-1，1]上的最大值为zmax=，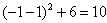
最小值为，
故当sin2x=-1时，y取得最大值10；当sin2x=1时，y取得最小值6。