问题
解答题
已知二次函数f(x)=ax2+bx,﹣1≤f(﹣1)≤1,3≤f(1)≤5.
(1)求a,b的取值范围;
(2)求f(2)的取值范围.
答案
解:(1)因为﹣1≤f(﹣1)≤1,3≤f(1)≤5.
所以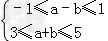
所以1≤a≤3;1≤b≤3;
(2)因为f(2)=4a+2b,
4a+2b=(a﹣b)+3(a+b),
因为 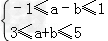 ,
,
所以8≤(a﹣b)+3(a+b)≤16,
即8≤f(2)≤16.
已知二次函数f(x)=ax2+bx,﹣1≤f(﹣1)≤1,3≤f(1)≤5.
(1)求a,b的取值范围;
(2)求f(2)的取值范围.
解:(1)因为﹣1≤f(﹣1)≤1,3≤f(1)≤5.
所以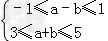
所以1≤a≤3;1≤b≤3;
(2)因为f(2)=4a+2b,
4a+2b=(a﹣b)+3(a+b),
因为 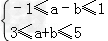 ,
,
所以8≤(a﹣b)+3(a+b)≤16,
即8≤f(2)≤16.