问题
解答题
已知函数f（x）=x2+ax+b，且对任意的实数x都有f（1+x）=f（1-x）成立，
（1）求实数a的值；
（2）利用单调性的定义证明函数f（x）在区间[1，+∞)上是增函数。
答案
解：（1）由f（1+x）=f（1-x）得（1+x）2+a（1+x）+b=（1-x）2+a（1-x）+b，
整理得：（a+2）x=0，
由于对任意的x都成立，
∴a=-2。
（2）根据（1）可知f（x）=x2-2x+b，
下面证明函数f（x）在区间[1，+∞上是增函数，
设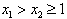
，
则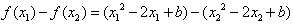
，
∵
，
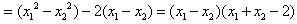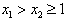则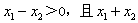
-2＞2-2=0，
∴
，
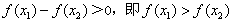故函数f（x）在区间[1，+∞上是增函数。