问题
填空题
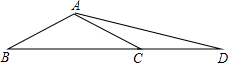
在△ABC中，AB＝AC，∠BAC＝120°，延长BC到D，使CD＝AC，则∠CDA＝ 度.
答案
15．
题目分析：根据三角形内角和定理和等腰三角形的性质可得∠ACB的度数，再根据等腰三角形的性质和三角形外角与内角之间的关系可得∠CDA的度数：
∵在△ABC中，AB=AC，∠BAC=120°，
∴∠ACB=（180°-120°）÷2=30°，
∵CD=AC，
∴∠CDA=30°÷2=15°．
搜题请搜索小程序“爱下问搜题”