问题
解答题
已知函数f(x)=1+|x-a|-x2是偶函数,当x为何值时,f(x)有最大值?其最大值为多少?
答案
解:∵f(x)的定义域为R,且f(x)是偶函数,
∴f(-x)=f(x)对任意x∈R都成立,
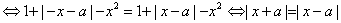 对任意x∈R都成立,
对任意x∈R都成立,
∴a=0,
从而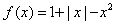 ,
,
令t=|x|,∵x∈R,
∴t≥0,且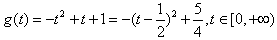 ,
,
∴当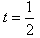 时,g(t)有最大值
时,g(t)有最大值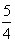 ,
,
∴当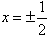 时,f(x)有最大值,且最大值为
时,f(x)有最大值,且最大值为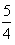 。
。
已知函数f(x)=1+|x-a|-x2是偶函数,当x为何值时,f(x)有最大值?其最大值为多少?
解:∵f(x)的定义域为R,且f(x)是偶函数,
∴f(-x)=f(x)对任意x∈R都成立,
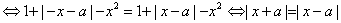 对任意x∈R都成立,
对任意x∈R都成立,
∴a=0,
从而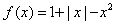 ,
,
令t=|x|,∵x∈R,
∴t≥0,且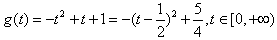 ,
,
∴当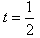 时,g(t)有最大值
时,g(t)有最大值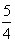 ,
,
∴当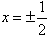 时,f(x)有最大值,且最大值为
时,f(x)有最大值,且最大值为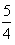 。
。