问题
解答题
已知函数f（x）=ax2-2ax+2+b（a＞0）在区间[2，3]上的值域为[2，5]，
（1）求a，b的值；
（2）若关于x的函数g（x）=f（x）-（m+1）x在[2，4]上为单调函数，求m的取值范围。
答案
解：（1）∵a＞0，
∴所以抛物线开口向上且对称轴为x=1，
∴函数f(x)在[2，3]上单调递增，
由条件得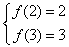
，即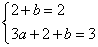
，
解得a=1，b=0；
（2）由（1）知a=1，b=0，
∴f(x)=x2-2x+2，从而g(x)=x2-(m+3)x+2，
若g(x)在[2，4]上递增，则对称轴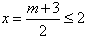
，解得m≤1；
若g(x)在[2，4]上递减，则对称轴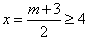
，解得m≥5；
故所求m的取值范围是m≥5或m≤1。