问题
解答题
函数f（x）=-x2+2ax+1-a在区间[0，1]上有最大值2，求实数a的值。
答案
解：对称轴x=a，
当a＜0，[0，1]是f（x）的递减区间，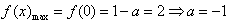
；
当a＞1，[0，1]是f（x）的递增区间，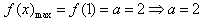
；
当0≤a≤1时，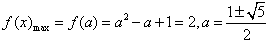
，与0≤a≤1矛盾；
所以a=-1或2。
搜题请搜索小程序“爱下问搜题”
函数f（x）=-x2+2ax+1-a在区间[0，1]上有最大值2，求实数a的值。
解：对称轴x=a，
当a＜0，[0，1]是f（x）的递减区间，；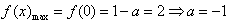
当a＞1，[0，1]是f（x）的递增区间，；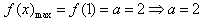
当0≤a≤1时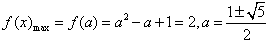，，与0≤a≤1矛盾；
所以a=-1或2。