问题
解答题
将容量为100的样本拆分为10组，若前7组频率之和为0.79，而剩下的三组的频数成等比数列，其公比为整数且不为1，求剩下的三组中频数最大的一组的频率．
答案
设三组数分别为a，aq，aq2，（a，q∈N*，q＞1），则
a+aq+aq2=21，即a（1+q+q2）=21，
又因为1+q+q2＞3，所以a=
＜7，21 1+q+q2
又因为q是整数，∴a是21的正约数，故a=1或a=3，
当a=1时，可得1+q+q2=21，即（q-4）（q+5）=0，
解得q=4，或q=-5（舍去），
频数最大的一组是aq2=16，频率是
=0.16；16 100
当a=3时，可得1+q+q2=7，即（q-2）（q+3）=0，
解得q=2，或q=-3（舍去），
频数最大的一组是aq2=12，频率是
=0.12．12 100
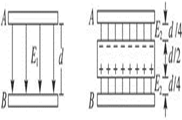（1）合上S; （2）在两板中央插入厚为
的金属板（3）打开S（4）抽出金属板. 则此时电容器两板间的电势差为( )