问题
解答题
已知函数f（x）=ax2﹣2x+1，（a∈R）．
（1）讨论函数f（x）的单调性；
（2）解关于x的方程f（x）=0；
（3）当a≥1时，f（x）在[2，4]上的最小值为5，求a的值．
答案
解：（1）当a=0时，函数f（x）=﹣2x+1在（﹣∞，+∞）上为减函数；
当a＞0时，函数f（x）=ax2﹣2x+1开口向上，对称轴为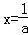
∴函数f（x）在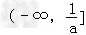
上为减函数，在
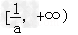上为增函数
当a＜0，函数f（x）=ax2﹣2x+1开口向下，对称轴为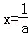
∴函数f（x）在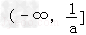
上为增函数，在
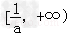上为减函数
（2）方程f（x）=ax2﹣2x+1=0，当a=0时，方程﹣2x+1=0有1个实根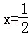
，
当a≠0时，△=4﹣4a
①若△＜0，即a＞1时，方程ax2﹣2x+1=0没有实根
②若△=0，即a=1时，方程ax2﹣2x+1=0有1个实根x=1
③若△＞0，即a＜1，且a≠0时，方程ax2﹣2x+1=0有2个实根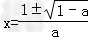
综上：当a＞1时，方程f（x）=0没有实根
当a=0时，方程f（x）=0有1个实根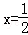
当a=1时，方程f（x）=0有1个实根x=1
当a＜1，且a≠0时，方程f（x）=0有2个实根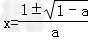
（3）当a≥1时，函数f（x）=ax2﹣2x+1开口向上，对称轴为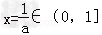
∴f（x）在区间[2，4]上为增函数
∴f（x）min=f（2）=4a﹣3=5，得a=2
