问题
解答题
已知函数f（x）=3x2-6x-5。
（Ⅰ）求不等式f（x）>4的解集；
（Ⅱ）设g（x）=f（x）-2x2+mx，其中m∈R，求g（x）在区间[1，3]上的最小值；
（Ⅲ）若对于任意的a∈[1，2]，关于x的不等式f（x）≤x2-（2a+6）x+a+b在[1，3]上恒成立，求实数b的取值范围。
答案
解：（Ⅰ）f（x）>4，即3x2-6x-9>0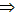
x2-2x- 3>0（x-3）（x+1）>0
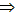x＜-1或x>3；
（Ⅱ）g（x）=f（x）-2x2+mx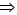
g（x）=x2+（m-6）x-5，
当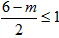
，即 m≥4时，g（x）min= g（1）=m-10；
当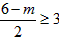
，即m≤0时，g（x）min=g（3）=3m-14：
当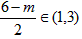
，即0＜m＜4时，g（x）min=
；
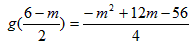（Ⅲ）设h（x）=x2-（2a+6）x+a+b，
h（x）min=-a2-5a+b-9，而a∈[1，2]，
∴当a=2时，h（x）取最小值，
∴当a=2时，有f（x）≤x2-（2a+6）x+a+b，则b≥2x2+4x-7=2（x+1）2-9=h'（x），
又∵x∈[1，3]，
∴b≥h'（3）=23。