问题
解答题
已知函数f（x）=x2﹣（a2﹣a）x﹣2
（1）若当x∈[1，3]时，f（x）为单调函数，求a的取值范围；
（2）求函数f（x）在[2，4]上的最大值g（a）；
（3）求g（a）的最大值．
答案
解：（1）∵函数f（x）=x2﹣（a2﹣a）x﹣2的图象是开口方向朝上，
以x=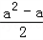
为对称轴的抛物线若当x∈[1，3]时，f（x）为单调函数，
则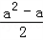
≤1，或
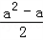≧3
解得a≤﹣2，或﹣1≤a≤2，或a≥3
故a的取值范围为（﹣∞，﹣2]∪[﹣1，2]∪[3，+∞）
（2）当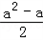
≧3，
即a≤﹣2，或a≧3时，
f（x）在[2，4]上的最大值
g（a）=f（2）=﹣2（a2﹣a）+2；
当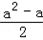
＜3，即﹣2＜a＜3时，
f（x）在[2，4]上的最大值
g（a）=f（4）=﹣4（a2﹣a）+14；
故g（a）=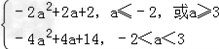
（3）由（2）得当a≤﹣2，或a≥3时，
g（a）的最大值为﹣10
当﹣2＜a＜3时g（a）的最大值为15
故g（a）的最大值为15