数列{an}中，a1=2，an+1=an+cn(c是常数，n=1，2，3，…)，

问题解答题

数列{a_n}中，a₁=2，a_n+1=a_n+cn(c是常数，n=1，2，3，…)，且a₁，a₂，a₃成公比不为1的等比数列，

(Ⅰ)求c的值；

(Ⅱ)求{a_n}的通项公式．

答案

解：(Ⅰ)a₁=2，a₂=2+c，a₃=2+3c，

因为a₁，a₂，a₃成等比数列，

所以(2+c)²=2(2+3c)，解得c=0或c=2，

当c=0时，a₁=a₂=a₃，不符合题意舍去，故c=2．

(Ⅱ)当n≥2时，由于a₂-a₁=c，a₃-a₂=2c，…，a_n-a_n-1=(n-1)c，

所以，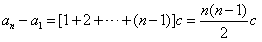

又a₁=2，c=2，

故a_n=2+n(n-1)=n²-n+2(n=2，3，…)，

当n=1时，上式也成立，

所以a_n=n²-n+2（n=1，2，…)。