问题
解答题
已知二次函数f(x)满足f(x+1)+f(x﹣1)=2x2﹣4x;
(1)求f(x)的解析式
(2)求当x∈[0,a](a为大于0的常数)时f(x)的最小值.
答案
解:(1)设f(x)=ax2+bx+c(a≠0),则有
f(x+1)+f(x﹣1)=2ax2+2bx+2a+2c=2x2﹣4x 对任意实数x恒成立
∴ 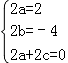
解之得a=1,b=﹣2,c=﹣1
∴f(x)=x2﹣2x﹣1
(2)当0<a<1时,f(x)的最小值为f(a)=a2﹣2a﹣1
当a≥1时,f(x)的最小值为f(1)=﹣2
