问题
解答题
设f(x)为二次函数,且f(1)=1,f(x+1)﹣f(x)=1﹣4x.
(1)求f(x)的解析式;
(2)设g(x)=f(x)﹣x﹣a,若函数g(x)在实数R上没有零点,求a的取值范围.
答案
解:(1)设f(x)=ax2+bx+c
则f(x+1)﹣f(x)=2ax+a+b,
∵f(x+1)﹣f(x)=1﹣4x
∴2ax+a+b=1﹣4x对一切x∈R成立.
∴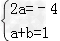
∴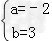 ,
,
又∵f(1)=1,
∴a+b+c=1,
∴c=0.
∴f(x)=﹣2x2+3x
(2)g(x)=f(x)﹣x﹣a=﹣2x2+2x﹣a,
函数g(x)在实数R上没有零点,故△=4﹣8a<0,
解之得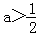

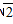 /2
/2