问题
解答题
在数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2,q≠0),
(1)设bn=an+1-an(n∈N*),证明{bn}是等比数列;
(2)求数列{an}的通项公式。
答案
(1)证明: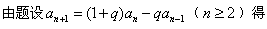
 ,即
,即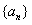 ,
,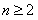 ,
,
又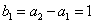 ,q≠0,
,q≠0,
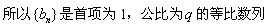 。
。
(2)解:由(1)知,
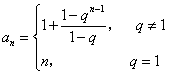 ,
,
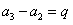 ,
,
……
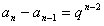 ,(
,(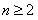 )
)
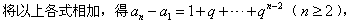
所以当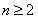 时,
时,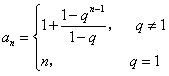 ,
,
上式对n=1显然成立。
所以,数列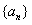 的通项公式为
的通项公式为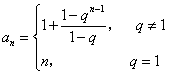 。
。
在数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2,q≠0),
(1)设bn=an+1-an(n∈N*),证明{bn}是等比数列;
(2)求数列{an}的通项公式。
(1)证明: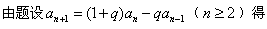
 ,即
,即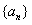 ,
,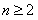 ,
,
又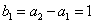 ,q≠0,
,q≠0,
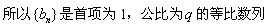 。
。
(2)解:由(1)知,
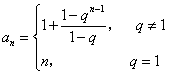 ,
,
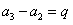 ,
,
……
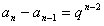 ,(
,(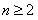 )
)
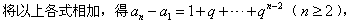
所以当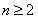 时,
时,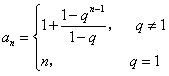 ,
,
上式对n=1显然成立。
所以,数列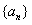 的通项公式为
的通项公式为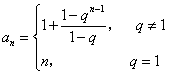 。
。