问题
解答题
已知函数f（x）和g（x）的图象关于原点对称，且f（x）=x2+2x．
（1）求函数g（x）的解析式；
（2）λ≠﹣1，若h（x）=g（x）﹣λf（x）+1在x∈[﹣1，1]上是增函数，求实数λ的取值范围．
答案
解：（1）设函数y=f（x）的图象上任意一点Q（x0，y0）关于原点的对称点为P（x，y），
则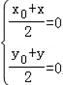
，即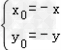
∵点Q（x0，y0）在函数y=f（x）的图象上
∴﹣y=x2﹣2x，即y=﹣x2+2x，
故g（x）=﹣x2+2x
（2）h（x）=﹣（1+λ）x2+2（1﹣λ）x+1
其对称轴方程为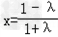
．
i）当λ＜﹣1时，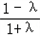
≤﹣1，解得λ＜﹣1
ii）当λ＞﹣1时，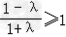
，解得﹣1＜λ≤0．
综上，λ≤0且λ≠﹣1